Modeling pragmatic inference

Chapter 2: Enriching the literal interpretations

Application 1: Scalar implicature

Scalar implicature stands as the poster child of pragmatic inference. Utterances are strengthened—via implicature—from a relatively weak literal interpretation to a pragmatic interpretation that goes beyond the literal semantics: “Some of the apples are red,” an utterance compatible with all of the apples being red, gets strengthened to “Some but not all of the apples are red.” The mechanisms underlying this process have been discussed at length. reft:goodmanstuhlmuller2013 apply an RSA treatment to the phenomenon and formally articulate the model by which scalar implicatures get calculated.

Assume a world with three apples; zero, one, two, or three of those apples may be red:

// possible states of the world
var states = [0, 1, 2, 3]
var statePrior = function() {
  return uniformDraw(states)
}
statePrior() // sample a state

Exercises:

Try visualizing statePrior() by drawing many samples and plotting the output (hint: you’ll need to use the repeat() function, which has a strange syntax that is documented here).

Try visualizing statePrior() by wrapping it in Infer (à la our \(L_0\) model).

Next, assume that speakers may describe the current state of the world in one of three ways:

// possible utterances
var utterancePrior = function() {
  return uniformDraw(['all', 'some', 'none'])
}

// meaning function to interpret the utterances
var literalMeanings = {
  all: function(state) { return state === 3; },
  some: function(state) { return state > 0; },
  none: function(state) { return state === 0; }
}

var utt = utterancePrior() // sample an utterance
var meaning = literalMeanings[utt] // get its meaning
display([utt, meaning(3)]) // apply meaning to state = 3

Exercise: Interpret the output of the above code box. (Run several times.)

Putting state priors and semantics together, we can implement the behavior of the literal listener. The literal listener will interpret messages by assigning probability 0 to each state where the observed message is false, and the same uniform probability to each true state.

// code for state prior and semantics as before
///fold:
// possible states of the world
var states = [0, 1, 2, 3]
var statePrior = function() {
  return uniformDraw(states)
};

// possible utterances
var utterancePrior = function() {
  return uniformDraw(['all', 'some', 'none']);
};

// meaning function to interpret the utterances
var literalMeanings = {
  all: function(state) { return state === 3; },
  some: function(state) { return state > 0; },
  none: function(state) { return state === 0; }
};
///

// literal listener
var literalListener = function(utt) {
  return Infer({model: function(){
    var state = uniformDraw(states)
    var meaning = literalMeanings[utt]
    condition(meaning(state))
    return state
  }}
)}

display("literal listener's interpretation of 'some':")
viz(literalListener("some"))

Next, let’s have a look at the speaker’s behavior. Intuitively put, in the vanilla RSA model, the speaker will never choose a false message; the speaker chooses among the true utterances by prioritizing those with the strongest meaning (see Appendix Chapter 2). You can verify this behavior with the following code.

// code for state prior, semantics and literal listener as before
///fold:
// possible states of the world
var states = [0, 1, 2, 3]
var statePrior = function() {
  return uniformDraw(states)
}

// possible utterances
var utterancePrior = function() {
  return uniformDraw(['all', 'some', 'none'])
}

// cost function for utterances
var cost = function(utterance){
  utterance == "all" ? 1 :
  utterance == "some" ? 1 :
  utterance == "none" ? 1 :
  0
}

// meaning function to interpret the utterances
var literalMeanings = {
  all: function(state) { return state === 3; },
  some: function(state) { return state > 0; },
  none: function(state) { return state === 0; }
}

// literal listener
var literalListener = function(utt) {
  return Infer({model: function(){
    var state = uniformDraw(states)
    var meaning = literalMeanings[utt]
    condition(meaning(state))
    return state
  }}
)}
///

// set speaker optimality
var alpha = 1

// pragmatic speaker
var speaker = function(state) {
  return Infer({model: function(){
    var utt = utterancePrior()
    factor(alpha * (literalListener(utt).score(state) - cost(utt)))
    return utt
  }})
}

display("speaker's production probabilities for state 3:")
viz(speaker(3))

With this knowledge about the communication scenario—crucially, the availability of the “all” alternative utterance—a pragmatic listener is able to infer from the “some” utterance that a state in which the speaker would not have used the “all” utterance is more likely than one in which she would. The following code—a complete vanilla RSA model for scalar implicatures—implements the pragmatic listener. (Technical note: Below, cache is used to save the results of the various Bayesian inferences being performed, which increases computational efficiency when dealing with nested inferences.)

// possible states of the world
var states = [0, 1, 2, 3]
var statePrior = function() {
  return uniformDraw(states)
}

// possible utterances
var utterancePrior = function() {
  return uniformDraw(['all', 'some', 'none'])
}

// cost function for utterances
var cost = function(utterance){
  utterance == "all" ? 1 :
  utterance == "some" ? 1 :
  utterance == "none" ? 1 :
  0
}

// meaning function to interpret the utterances
var literalMeanings = {
  all: function(state) { return state === 3; },
  some: function(state) { return state > 0; },
  none: function(state) { return state === 0; }
}

// literal listener
var literalListener = cache(function(utt) {
  return Infer({model: function(){
    var state = uniformDraw(states)
    var meaning = literalMeanings[utt]
    condition(meaning(state))
    return state
  }})
})

// set speaker optimality
var alpha = 1

// pragmatic speaker
var speaker = cache(function(state) {
  return Infer({model: function(){
    var utt = utterancePrior()
    factor(alpha * (literalListener(utt).score(state) - cost(utt)))
    return utt
  }})
})

// pragmatic listener
var pragmaticListener = cache(function(utt) {
  return Infer({model: function(){
    var state = statePrior()
    observe(speaker(state),utt)
    return state
  }})
})

display("pragmatic listener's interpretation of 'some':")
viz(pragmaticListener('some'))

Exercises:

Explore what happens if you make the speaker less optimal.

Subtract one of the utterances. What changed?

Add a new utterance. What changed?

Check what would happen if ‘some’ literally meant some-but-not-all (hint: use != to assert that two values are not equal).

Change the relative prior probabilities of the various states and see what happens to model predictions.

Application 2: Scalar implicature and speaker knowledge

Section overview

Capturing scalar implicature within the RSA framework might not induce waves of excitement. However, by implementing implicature-calculation within a formal model of communication, we can also capture its interactions with other pragmatic factors. reft:GoodmanStuhlmuller2013Impl explored a model of what happens when the speaker possibly only has partial knowledge about the state of the world. Below, we explore their model, taking into account the listener’s beliefs about the speaker’s (possibly uncertain) beliefs about the world. We then go beyond the work of reft:GoodmanStuhlmuller2013Impl and study also the way these higher-order listener beliefs about the speaker’s knowledge may change when hearing an utterance.

Setting the scene

Suppose a speaker says: “Some of the apples are red.” If you know that there are 3 apples in total, but that the speaker has only observed two of them, how likely do you think it is that 0, 1, 2 or 3 of the apples are red? This is the question that reft:GoodmanStuhlmuller2013Impl address (Fig. 1 below).

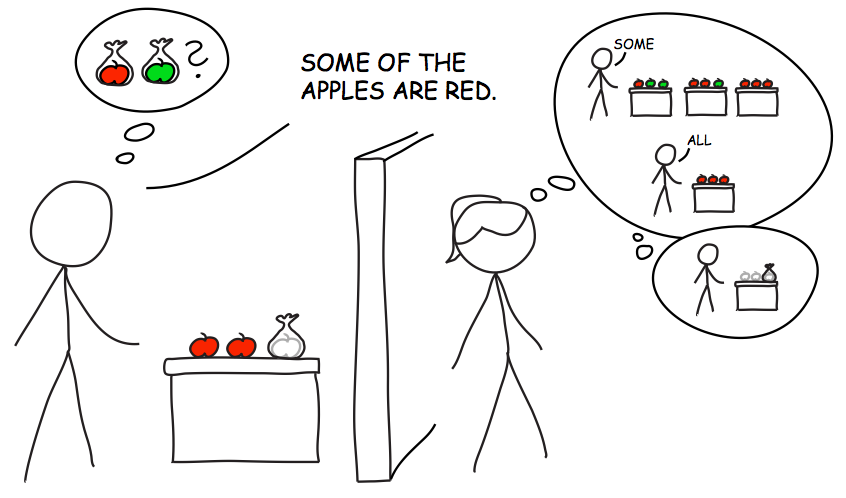
Example communication scenario from Goodman and Stuhlmüller: How will the listener interpret the speaker’s utterance? How will this change if she knows that he can see only two of the objects?

Fig. 1: Example communication scenario from Goodman and Stuhlmüller: How will the listener interpret the speaker’s utterance? How will this change if she knows that he can see only two of the objects?

Towards an implementation, let’s introduce some terminology and some notation. The total number of apples is \(n\), of which \(0 \le s \le n\) are red. We call \(s\) the state of the world. The speaker knows \(n\) (as does the listener) but the speaker might not know the true state \(s\), because she might only observe some of the apples’ colors. Concretely, the speaker might only have seen (i.e., accessed) some of the apples; of those apples that were accessed, the speaker might have observed that some of them were red. The model of reft:GoodmanStuhlmuller2013Impl assumes that the listener knows how many apples the speaker saw (i.e., the speaker’s access \(a\)). We will first look at this model, and then generalize to the case where the listener must also infer \(a\) from the speaker’s utterance.

The extended Scalar Implicature model

In the extended Scalar Implicature model of reft:GoodmanStuhlmuller2013Impl, the pragmatic listener infers the true state \(s\) of the world not only on the basis of the observed utterance, but also the speaker’s epistemic access \(a\):

\[P_{L_{1}}(s\mid u, a) \propto P_{S_{1}}(u\mid s, a) \cdot P(s)\]

where

\[P_{S_{1}}(u\mid s, a) = \sum_o P_{S_{1}}(u \mid o, a) \cdot P(o \mid s, a)\]

is obtained from marginalizing out the possible observations \(o\).

// pragmatic listener
var pragmaticListener = cache(function(utt,access) {
  return Infer({model: function(){
    var state = statePrior()
    observe(speaker(access,state),utt)
    return numTrue(state)
  }})
});

We have to enrich the speaker model: first the speaker makes an observation \(o\) of the true state \(s\) with access \(a\). On the basis of this observation, the speaker infers \(s\).

///fold:
// tally up the state
var numTrue = function(state) {
  var fun = function(x) {
    x ? 1 : 0
  }
  return sum(map(fun,state))
}
///

// red apple base rate
var baserate = 0.8

// state builder
var statePrior = function() {
  var s1 = flip(baserate)
  var s2 = flip(baserate)
  var s3 = flip(baserate)
  return [s1,s2,s3]
}

// speaker belief function
var belief = function(actualState, access) {
  var fun = function(access_val,state_val) {
    return access_val ? state_val : uniformDraw(statePrior())
  }
  return map2(fun, access, actualState);
}

print("1000 runs of the speaker's belief function:")

viz.auto(repeat(1000,function() {
  numTrue(belief([true,true,true],[true,true,false]))
}))

Exercise: See what happens when you change the red apple base rate.

Given potential uncertainty about the world state \(s\), the speaker’s probabilistic production rule has to be adapted from the simpler formulation in Chapter I. This rule is now no longer a function of the true \(s\) (because, with limited access, the speaker might not know \(s\)), but of what the speaker believes \(s\) to be (i.e., the speaker’s epistemic state, given the speaker’s access). In the case at hand, the speaker’s epistemic state \(P_{S_{1}}(\cdot \mid o,a) \in \Delta(S)\) is given by access \(a\) and observation \(o\), as in the belief model implemented just above.

Even if the speaker is uncertain about the state \(s\) after some partial observation \(o\) and \(a\), she would still seek to choose an utterance that maximizes information flow. There are several ways in which we can combine speaker uncertainty (in the form of a probability distribution over \(s\)) and the speaker’s utility function, which remains unchanged from what we had before, so that utterances are chosen to minimize cost and maximize informativity:

\[U_{S_{1}}(u; s) = log(L_{0}(s\mid u)) - C(u)\]

The model implemented by reft:GoodmanStuhlmuller2013Impl assumes that the speaker samples a state \(s\) from her belief distribution and then samples an utterance based on the usual soft-maximization of informativity for that sampled state \(s\). The formulation of this choice rule looks cumbersome in mathematical notation but is particularly easy to implement. (Another variant that conservatively extends the vanilla RSA model’s assumption of rational agency is implemented in the next section. See also the discussion in the exercises below.)

\[P_{S_{1}}(u\mid o, a) \propto P_{S_{1}}(s\mid o, a) \ P_{S_{1}}(u \mid s)\] \[P_{S_{1}}(u \mid s) \propto exp(\alpha[U(u; s)])\]

// pragmatic speaker
var speaker = cache(function(access,state) {
  return Infer({model: function(){
    var utterance = utterancePrior()
    var beliefState = belief(state,access)
    factor(alpha * (literalListener(utterance).score(beliefState) - cost(utterance)))
    return utterance
  }})
});

The intuition (which Goodman and Stuhlmüller validate experimentally) is that in cases where the speaker has partial knowledge access (say, she knows about only two out of three relevant apples), the listener will be less likely to calculate the implicature (because he knows that the speaker doesn’t have the evidence to back up the strengthened meaning).

///fold:
// tally up the state
var numTrue = function(state) {
  var fun = function(x) {
    x ? 1 : 0
  }
  return sum(map(fun,state))
}

// possible states of the world
var states = [[true,true,true], 
              [false,true,true], 
              [true,false,true],
              [true,true,false],    
              [false,false,true],
              [false,true,false],
              [true,false,false],
              [false,false,false]]
///

// Here is the code from the Goodman and Stuhlmüller speaker-access SI model

// red apple base rate
var baserate = 0.8

// state prior
var statePrior = function() {
  var s1 = flip(baserate)
  var s2 = flip(baserate)
  var s3 = flip(baserate)
  return [s1,s2,s3]
}

// speaker belief function
var belief = function(actualState, access) {
  var fun = function(access_val,state_val) {
    return access_val ? state_val : uniformDraw(statePrior())
  }
  return map2(fun, access, actualState);
}

// utterance prior
var utterancePrior = function() {
  uniformDraw(['all','some','none'])
}

// cost function for utterances
var cost = function(utterance){
  utterance == "all" ? 1 :
  utterance == "some" ? 1 :
  utterance == "none" ? 1 :
  0
}

// meaning funtion to interpret utterances
var literalMeanings = {
  all: function(state) { return all(function(s){s}, state); },
  some: function(state) { return any(function(s){s}, state); },
  none: function(state) { return all(function(s){s==false}, state); }
};

// literal listener
var literalListener = cache(function(utt) {
  return Infer({model: function(){
    var state = uniformDraw(states)
    var meaning = literalMeanings[utt]
    condition(meaning(state))
    return state
  }})
});

// set speaker optimality
var alpha = 1

// pragmatic speaker
var speaker = cache(function(access,state) {
  return Infer({model: function(){
    var utterance = utterancePrior()
    var beliefState = belief(state,access)
    factor(alpha * (literalListener(utterance).score(beliefState) - cost(utterance)))
    return utterance
  }})
});

// pragmatic listener
var pragmaticListener = cache(function(utt,access) {
  return Infer({model: function(){
    var state = statePrior()
    observe(speaker(access,state),utt)
    return numTrue(state)
  }})
});

print("pragmatic listener for a full-access speaker:")
viz.auto(pragmaticListener('some',[true,true,true]))
print("pragmatic listener for a partial-access speaker:")
viz.auto(pragmaticListener('some',[true,true,false]))

Exercises:

Check the predictions for the other possible knowledge states.

Compare the full-access predictions with the predictions from the simpler scalar implicature model above. Why are the predictions of the two models different? How can you get the model predictions to converge? (Hint: first try to align the predictions of the simpler model with those of the knowledge model, then try aligning the predictions of the knowledge model with those of the simpler model.)

Notice that the listener assigns some positive probability to the true state being 0, even when it is shared knowledge that the speaker saw 2 apples and said “some”. Why is this puzzling? (Think about the Gricean Maxim of Quality demanding that speakers not say what they lack sufficient evidence for.) Look at the speaker choice function implemented above and explain why this behavior takes place.

We have seen how the RSA framework can implement the mechanism whereby utterance interpretations are strengthened. Through an interaction between what was said, what could have been said, and what all of those things literally mean, the model delivers scalar implicature. And by taking into account awareness of the speaker’s knowledge, the model successfully blocks implicatures in those cases where listeners are unlikely to access them.

Joint-inferences of world state and speaker competence

In this section we further extend the model of Goodman & Stuhlmüller to also consider the listener’s uncertainty about \(a\), the number of apples that the speaker actually observed. This has interesting theoretical implications.

Many traditional approaches to scalar implicature calculation follow what reft:Geurts2010:Quantity-Implic calls the standard recipe:

the speaker used some
one reason why the speaker did not use all instead is that she does not know whether it is true
the speaker is assumed to be epistemically competent, i.e., she knows whether it is “all” or “some but not all” [Competence Assumption]
so, she knows that the all sentence is actually false
if the speaker knows it, it must be true (by veridicality of knowledge)

Crucially, the standard recipe requires the Competence Assumption to derive a strong scalar implicature about the way the world is. Without the competence assumption, we only derive the weak epistemic implicature: that the speaker does not know that all is true.

From a probabilistic perspective, this is way too simple. Probabilistic modeling, aided by probabilistic programming tools, lets us explore a richer and more intuitive picture. In this picture, the listener may have probabilistic beliefs about the degree to which the speaker is in possession of the relevant facts. While these gradient prior beliefs of the listener about the speaker’s likely competence matter to the interpretation of an utterance, hearing an utterance may also dynamically change these beliefs.

As before, let \(n\) be the total number of apples of which \(0 \le s \le n\) are red. The speaker has access to \(0 \le a \le n\) apples, of which she observes \(0 \le o \le a\) to be red. Previously, we looked at a case where the listener knows \(a\). Here, we look at the (more natural) case where the listener must infer the degree to which the speaker is knowledgable (competent) from prior knowledge and the speaker’s utterance.

If the speaker communicates her belief state with a statement like “Some of the apples are red”, the listener performs a joint inference of the true world state \(s\), the access \(a\) and the observation \(o\):

\[P_{L_{1}}(s, a, o \mid u) \propto P_{S_{1}}(u\mid a, o) \cdot P(s,a,o)\]

// pragmatic listener
var pragmaticListener = function(utt) {
  return Infer({model: function(){
    var state = statePrior()
    var access = accessPrior()
    var observed = observePrior()
    factor(Math.log(hypergeometricPMF(observed, total_apples,
                                      state, access)))
    observe(speaker(access, observed), utt)
    return {state, access, observed}
  }})
}

This formulation of the pragmatic listener differs in two respects from the previous. First, the pragmatic listener also has a (possibly uncertain) prior belief about \(a\), which we can think of as prior knowledge of the likely extent of the speaker’s competence. Second, the new formulation also refers to a hypergeometric distribution, which we use as a more general way of representing the speaker’s (possibly partial) beliefs.

Here is how to understand the speaker belief model in terms of a hypergeometric distribution. We first look at the speaker’s prior beliefs about \(s\): what does a speaker believe about the world state \(s\) after, say, having access to \(a\) out of \(n\) apples and seeing that \(o\) of the accessed apples are red? These beliefs are given by a binomial distribution with a fixed base rate of redness: intuitively put, each apple has a chance base_rate of being red; how many red apples do we expect given that we have \(n\) apples in total?

// total number of apples (known by speaker and listener)
var total_apples = 3

// red apple base rate
var base_rate_red = 0.8

// state = how many apples of 'total_apples' are red?
var statePrior = function() {
  binomial({p: base_rate_red, n: total_apples})
}

Infer(statePrior)

Exercise: Play around with total_apples and base_rate_red to get good intuitions about the state prior for different parameters. (For which values of total_apples and base_rate_red would it be better to take more samples for a more precise visualization?)

A world state \(s\) gives the true, actual number of red apples. If the world state was known to the speaker (and the total number of apples \(n\)), her beliefs for any value of \(o\) for a given \(a\) are given by a so-called hypergeometric distribution. The hypergeometric distribution gives the probability of retrieving \(o\) red balls when drawing \(a\) balls without replacement from an urn which contains \(n\) balls in total of which \(s\) are red. (This distribution is not implemented in WebPPL, so we implement its probability mass function by hand. Although this is tedious and the previous coding-by-hand might be more insightful, this formulation allows for easier manipulation of \(o\), \(a\) and \(s\) as actual numbers.)

var factorial = function(x) {
  if (x < 0) {return "input to factorial function must be non-negative"}
  return x == 0 ? 1 : x * factorial(x-1)
}

var binom = function(a, b) {
  var numerator = factorial(a)
  var denominator = factorial(a-b) *  factorial(b)
  return numerator / denominator
}

// urn contains N balls of which K are black
// and N-K are white; we draw n balls at random
// without replacement; what's the probability
// of obtaining k black balls?
var hypergeometricPMF = function(k,N,K,n) {
  k > Math.min(n, K) ? 0 :
  k < n+K-N ? 0 :       
  binom(K,k) * binom(N-K, n-k) / binom(N,n)
}

var hypergeometricSample = function(N,K,n) {
  var support = _.range(N+1) // possible values 0, ..., N
  var PMF = map(function(k) {hypergeometricPMF(k,N,K,n)}, support)
  categorical({vs: support, ps: PMF })    
}

var total_apples = 3, state = 2, access = 1;
Infer(function() {hypergeometricSample(total_apples, state, access)})

The prior over states and the hypergeometric distribution combine to give the speaker’s beliefs about world state \(s\) given access \(a\) and observation \(o\), using Bayes rule (and knowledge of the total number of apples \(n\)):

\[P_{S_1}(s \mid a, o) \propto \text{Hypergeometric}(o \mid s, a, n) \ \text{Binomial}(s \mid \text{baserate, n})\]

// code for hypergeometric 
///fold:
var factorial = function(x) {
  if (x < 0) {return "input to factorial function must be non-negative"}
  return x == 0 ? 1 : x * factorial(x-1)
}

var binom = function(a, b) {
  var numerator = factorial(a)
  var denominator = factorial(a-b) *  factorial(b)
  return numerator / denominator
}

// urn contains N balls of which K are black
// and N-K are white; we draw n balls at random
// without replacement; what's the probability
// of obtaining k black balls?
var hypergeometricPMF = function(k,N,K,n) {
  k > Math.min(n, K) ? 0 :
  k < n+K-N ? 0 :       
  binom(K,k) * binom(N-K, n-k) / binom(N,n)
}

var hypergeometricSample = function(N,K,n) {
  var support = _.range(N+1) // possible values 0, ..., N
  var PMF = map(function(k) {hypergeometricPMF(k,N,K,n)}, support)
  categorical({vs: support, ps: PMF })    
}
///

// total number of apples (known by speaker and listener)
var total_apples = 3

// red apple base rate
var base_rate_red = 0.8

// state = how many apples of 'total_apples' are red?
var statePrior = function() {
  binomial({p: base_rate_red, n: total_apples})
}

var belief = cache(function(access, observed){
  Infer({model: function() {
    var state = statePrior()
    var hyperg_sample = hypergeometricSample(total_apples,
                         state,
                         access)
    condition(hyperg_sample == observed)
    return state
  }}) 
})

viz(belief(2,1))

Exercises:

See what happens when you change the red apple base rate.

See what happens when you increase the number of total apples.

See what happens when you give the speaker more access and different numbers of observed red apples.

To combine the speaker’s beliefs \(P_{S_{1}}(\cdot \mid o,a) \in \Delta(S)\) about the world state, reft:GoodmanStuhlmuller2013Impl assumed a simple sampling-based method: the speaker sampled a state and considered what to say for it. While this is cognitively plausible, a fully rational agent would rather soft-maximize the expected utility under the given uncertainty:

\[P_{S_{1}}(u \mid o, a) \propto \exp(\alpha \ \mathbb{E}_{P_{S_{1}}(s \mid o, a)}[U(u; s)])\]

The speaker’s utility function remains unchanged:

\[U_{S_{1}}(u; s) = log(L_{0}(s\mid u)) - C(u)\]

// expected utilities
var get_EUs = function(access, observed, utterance){
  var EUs = sum(map(function(s) {
      var eu_at_state = Math.exp(belief(access, observed).score(s)) *
          literalListener(utterance).score(s)
      _.isNaN(eu_at_state) ? 0 : eu_at_state // convention here: 0*-Inf=0
    }, _.range(total_apples + 1)))
  return EUs
}

// pragmatic speaker
var speaker = function(access, observed) {
  return Infer({model: function(){
    var utterance = utterancePrior()
    var EUs = get_EUs(access, observed, utterance)
    factor(alpha * EUs)
    return utterance
  }})
}

An equivalent motivation for this speaker model is that the speaker chooses an utterance with the goal of minimizing the (Kullback-Leibler) divergence between her belief state \(P_{S_{1}}(\cdot \mid o,a)\) and that of the literal listener \(P_{L_0}(\cdot \mid u)\). Details are in appendix chapter II.

There is one important bit to notice about this definition. In the vanilla RSA model of the previous chapter, the speaker will never say anything false. The present conservative extension makes it so that an uncertain speaker will never use an utterance whose truth the speaker is not absolutely convinced of. In other words, as long as \(P_{S_{1}}(\cdot \mid o,a)\) puts positive probability on a state \(s\) for which utterance \(u\) is false, the speaker will never use \(u\) in epistemic state \(\langle o, a \rangle\). This is because \(\log P_{L_0}(s \mid u)\) is negative infinity if \(u\) is false of \(s\) and so the expected utility (which is a weighted sum) will be negative infinity as well, unless \(P_{S_{1}}(s \mid o,a) = 0\). As a consequence, we need to make sure in the model that the speaker always has something true to say for all pairs of \(a\) and \(o\). We do this by including a “null utterance”, which is like saying nothing. (See also chapter V and reft:PottsLassiter2016:Embedded-implic for similar uses of a “null utterance”.)

Adding a set of utterances, an utterance prior and the literal listener, we obtain a full speaker model.

// red apple base rate
var total_apples = 3
var base_rate_red = 0.8

// state = how many apples of 'total_apples' are red?
var statePrior = function() {
  binomial({p: base_rate_red, n: total_apples})
}

// binomial-hypergeometric belief model
///fold:
var factorial = function(x) {
  if (x < 0) {return "input to factorial function must be non-negative"}
  return x == 0 ? 1 : x * factorial(x-1)
}

var binom = function(a, b) {
  var numerator = factorial(a)
  var denominator = factorial(a-b) *  factorial(b)
  return numerator / denominator
}

// urn contains N balls of which K are black
// and N-K are white; we draw n balls at random
// without replacement; what's the probability
// of obtaining k black balls?
var hypergeometricPMF = function(k,N,K,n) {
  k > Math.min(n, K) ? 0 :
  k < n+K-N ? 0 :
  binom(K,k) * binom(N-K, n-k) / binom(N,n)
}

var hypergeometricSample = function(N,K,n) {
  var support = _.range(N+1) // possible values 0, ..., N
  var PMF = map(function(k) {hypergeometricPMF(k,N,K,n)}, support)
  categorical({vs: support, ps: PMF })
}

var belief = cache(function(access, observed){
  Infer({model: function() {
    var state = statePrior()
    var hyperg_sample = hypergeometricSample(total_apples,
                         state,
                         access)
    condition(hyperg_sample == observed)
    return state
  }})
})
///

// utterance prior
var utterancePrior = function() {
  categorical({vs: ['all','some','none','null'],
               ps: [1,1,1,0.0000001]})
}

// meaning function to interpret utterances
var literalMeanings = {
  all:  function(state) { state == total_apples },
  some: function(state) { state > 0 },
  none: function(state) { state == 0 },
  null: function(state) { state >= 0 }
}

// literal listener
var literalListener = cache(function(utt) {
  return Infer({model: function(){
    var state = statePrior()
    var meaning = literalMeanings[utt]
    condition(meaning(state))
    return state
  }})
})

// set speaker optimality
var alpha = 1

// expected utilities
var get_EUs = function(access, observed, utterance){
  var EUs = sum(map(function(s) {
      var eu_at_state = Math.exp(belief(access, observed).score(s)) *
          literalListener(utterance).score(s)
      _.isNaN(eu_at_state) ? 0 : eu_at_state // convention here: 0*-Inf=0
    }, _.range(total_apples + 1)))
  return EUs
}

// pragmatic speaker
var speaker = cache(function(access, observed) {
  return Infer({model: function(){
    var utterance = utterancePrior()
    var EUs = get_EUs(access, observed, utterance)
    factor(alpha * EUs)
    return utterance
  }})
})

viz(speaker(2,1))

Exercises:

Test the speaker model for different parameter values. Also change total_apples and base_rate_red.

When does the speaker use the “null” utterance?

If the pragmatic listener does not know the number \(a\) of apples that the speaker saw, the listener can nevertheless infer likely values for \(a\), given an utterance. In fact, the listener can make a joint inference of \(s\), \(a\) and \(o\), all of which are unknown to him, but all of which feed into the speaker’s utterance probabilities. The posterior inference of \(a\) is particularly interesting because it is a probabilistic inference of the speaker’s competence, mediated by what the speaker said.

// red apple base rate
var total_apples = 3
var base_rate_red = 0.8

// state = how many apples of 'total_apples' are red?
var statePrior = function() {
  binomial({p: base_rate_red, n: total_apples})
}

// binomial-hypergeometric belief model
///fold:
var factorial = function(x) {
  if (x < 0) {return "input to factorial function must be non-negative"}
  return x == 0 ? 1 : x * factorial(x-1)
}

var binom = function(a, b) {
  var numerator = factorial(a)
  var denominator = factorial(a-b) *  factorial(b)
  return numerator / denominator
}

// urn contains N balls of which K are black
// and N-K are white; we draw n balls at random
// without replacement; what's the probability
// of obtaining k black balls?
var hypergeometricPMF = function(k,N,K,n) {
  k > Math.min(n, K) ? 0 :
  k < n+K-N ? 0 :
  binom(K,k) * binom(N-K, n-k) / binom(N,n)
}

var hypergeometricSample = function(N,K,n) {
  var support = _.range(N+1) // possible values 0, ..., N
  var PMF = map(function(k) {hypergeometricPMF(k,N,K,n)}, support)
  categorical({vs: support, ps: PMF })
}

var belief = cache(function(access, observed){
  Infer({model: function() {
    var state = statePrior()
    var hyperg_sample = hypergeometricSample(total_apples,
                         state,
                         access)
    condition(hyperg_sample == observed)
    return state
  }})
})
///

// speaker model (as before)
///fold:

// utterance prior
var utterancePrior = function() {
  categorical({vs: ['all','some','none','null'],
               ps: [1,1,1,0.0000001]})
}

// meaning function to interpret utterances
var literalMeanings = {
  all:  function(state) { state == total_apples },
  some: function(state) { state > 0 },
  none: function(state) { state == 0 },
  null: function(state) { state >= 0 }
}

// literal listener
var literalListener = cache(function(utt) {
  return Infer({model: function(){
    var state = statePrior()
    var meaning = literalMeanings[utt]
    condition(meaning(state))
    return state
  }})
})

// set speaker optimality
var alpha = 1

// expected utilities
var get_EUs = function(access, observed, utterance){
  var EUs = sum(map(function(s) {
      var eu_at_state = Math.exp(belief(access, observed).score(s)) *
          literalListener(utterance).score(s)
      _.isNaN(eu_at_state) ? 0 : eu_at_state // convention here: 0*-Inf=0
    }, _.range(total_apples + 1)))
  return EUs
}

// pragmatic speaker
var speaker = cache(function(access, observed) {
  return Infer({model: function(){
    var utterance = utterancePrior()
    var EUs = get_EUs(access, observed, utterance)
    factor(alpha * EUs)
    return utterance
  }})
})
///

var observePrior = function(){
  uniformDraw(_.range(total_apples + 1))
}

var accessPrior = function(){
  uniformDraw(_.range(total_apples + 1))
}

var pragmaticListener = cache(function(utt) {
  return Infer({method: "enumerate",
//                 strategy: "breadthFirst",
                model: function(){
    var state = statePrior()
    var access = accessPrior()
    var observed = observePrior()
    factor(Math.log(hypergeometricPMF(observed, total_apples,
                                      state, access)))
    observe(speaker(access, observed), utt)
    return {state, access, observed}
  }})
});

var pl = pragmaticListener("some")
display("Marginal beliefs about the true world state:")
viz(marginalize(pl, 'state'))
display("Marginal beliefs about how many apples the speaker observed in total:")
viz(marginalize(pl, 'access'))
display("Marginal beliefs about how many apples the speaker observed to be red:")
viz(marginalize(pl, 'observed'))

Exercises:

How would you describe the result of the code above? Does the pragmatic listener draw a scalar implicature from “some” to “some but not all”?

Does the pragmatic listener, after hearing “some”, increase or decrease his belief in the speaker’s competence?

What does the pragmatic listener infer about the speaker’s competence when he hears “all” or “none”?

Speculate about how the listener’s inferences about speaker competence might be influenced by the inclusion of further utterance alternatives.

Conclusion

In this chapter, we saw a simple model of scalar implicature calculation based on the vanilla RSA model. We then extended this model to also cover the speaker’s uncertainty, and eventually also the listener’s inferences about how likely the speaker is to be knowledgeable.

Within the RSA framework, speakers try to optimize information transmission. You might then think that the framework has nothing to say about situations where speakers produce utterances that are literally false, as in “I had to wait a million years to get a table last night!” In the next chapter, we’ll see how expanding the range of communicative goals of the speaker can lead listeners to infer nonliteral interpretations of utterances.

Table of Contents